Clio supplemento a Argonauta n. 7-12 2011

back to index
TRANSLATION
PAG. 1
The shape of the shells has attracted the admiration and interest of all people feel the wonders of nature. Classics Naturalists (Aristotle and Pliny the Younger) were very concerned with the problem of the shape of shells. Aristotle in his work has divided the molluscs: spirals, bivalves and cephalopods in Pliny's "Natural History" was interested in molluscs and shells. The shells, in particular, had caught his attention for their variety. In their descriptions he uses a long list of specific terms and many of these terms have been taken many centuries later, when we began to describe the species of shells to classify. However, one must arrive at 1600 for observations of the shapes of shells, in fact, a monk, "Father Buonanni" says: "The round shape is explained because it is easier to to walk around and fold over themselves. If you could play the shells as you would see a perfect conical body and its parts with the proportion of smaller and smaller circles always artificially decreased. "In the book of Father Buonanni meet many interesting observations. For example, the shape of the wound shells can also be justified in thinking that offers better grip when this animal springs must find a foothold to the force exerted by the foot: that is, if the animal was not
PAG. 2
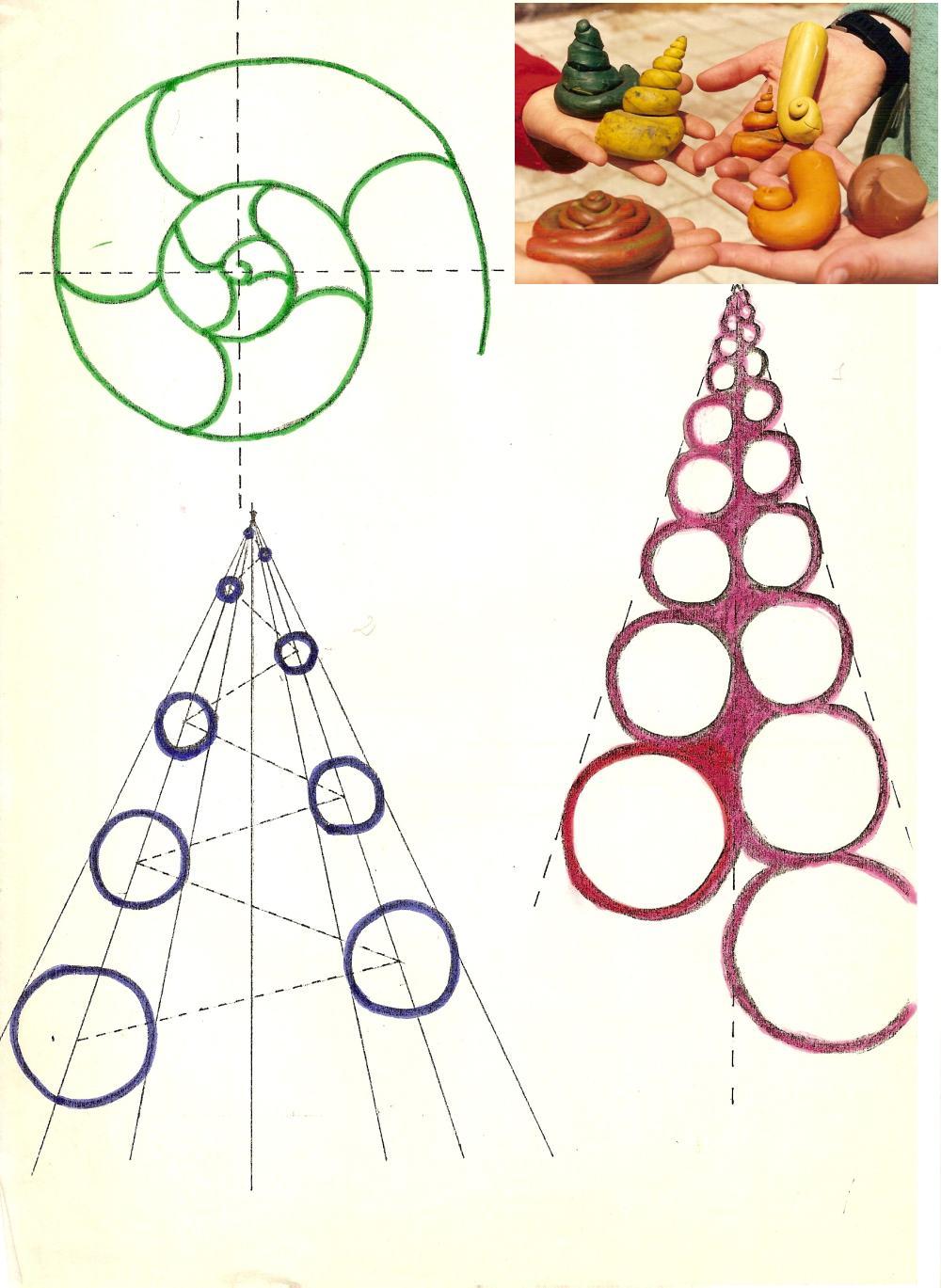
wrapped tend to fall out of the shell if it is pulled while the animal is under your foot. Between 1600 and 1700 so many comments about the shape of shells were made, but you should arrive in 1800 that there would be discussions on the shells of geometric and mathematical basis. Aristotle had already observed the spiral form. The spirals are more common: the spiral of Archimedes and the logarithmic spiral. The Archimedes spiral is a curve according to which one has a rope wound on a plane. It has a constant pitch, ie the distance p is the same in any point of the curve.
The shape of the shells has attracted the admiration and interest of all people feel the wonders of nature. Classics Naturalists (Aristotle and Pliny the Younger) were very concerned with the problem of the shape of shells. Aristotle in his work has divided the molluscs: spirals, bivalves and cephalopods in Pliny's "Natural History" was interested in molluscs and shells. The shells, in particular, had caught his attention for their variety. In their descriptions he uses a long list of specific terms and many of these terms have been taken many centuries later, when we began to describe the species of shells to classify. However, one must arrive at 1600 for observations of the shapes of shells, in fact, a monk, "Father Buonanni" says: "The round shape is explained because it is easier to to walk around and fold over themselves. If you could play the shells as you would see a perfect conical body and its parts with the proportion of smaller and smaller circles always artificially decreased. "In the book of Father Buonanni meet many interesting observations. For example, the shape of the wound shells can also be justified in thinking that offers better grip when this animal springs must find a foothold to the force exerted by the foot: that is, if the animal was not
PAG. 2
wrapped tend to fall out of the shell if it is pulled while the animal is under your foot. Between 1600 and 1700 so many comments about the shape of shells were made, but you should arrive in 1800 that there would be discussions on the shells of geometric and mathematical basis. Aristotle had already observed the spiral form. The spirals are more common: the spiral of Archimedes and the logarithmic spiral. The Archimedes spiral is a curve according to which one has a rope wound on a plane. It has a constant pitch, ie the distance p is the same in any point of the curve.
 |
 |
La forma delle conchiglie

|
The logarithmic spiral, however, does not have these characteristics, it is always constant the angle formed between the straight line tangent to the curve at the point where the curve meets a radius. In the spiral of Archimedes these rays coming out from the circle are in arithmetic progression is: OP4=OP3+p OP3=OP2+p OP2=OP1+p. In the logarithmic spiral, however, are in geometrical progression: OP4=OP3xq OP3=OP2xq OP2=OP1xq.
PAG. 3
To complete the scientific observations, using plasticine with the teacher we have built models of shells starting with conical shapes. We have achieved some examples of gastropods by winding on themselves, starting from the tip, around an imaginary axis, the conical shapes. We repeated the test with different lengths and sections of the cone to achieve different models. During the experiments we have found that we can identify a composition of movements of translation along the axis of the shell, the magnification (projection) of the section and simultaneous rotation about the axis. We also studied the molluscs were used by primitive men of the coast as an excellent food were always available and a good economic resource. In addition, the shells could be easily processed and then used as an object of exchange.
PAG. 3
To complete the scientific observations, using plasticine with the teacher we have built models of shells starting with conical shapes. We have achieved some examples of gastropods by winding on themselves, starting from the tip, around an imaginary axis, the conical shapes. We repeated the test with different lengths and sections of the cone to achieve different models. During the experiments we have found that we can identify a composition of movements of translation along the axis of the shell, the magnification (projection) of the section and simultaneous rotation about the axis. We also studied the molluscs were used by primitive men of the coast as an excellent food were always available and a good economic resource. In addition, the shells could be easily processed and then used as an object of exchange.